Tech: Guiding the search for ground robots (Part 1)

Guiding the search for ground robots turns out to be more difficult than anticipated.

Last time - which admittedly is a long time ago, so I don't blame you for not remembering - I talked about modelling and simulating the ground robots. I talked about how this was big deal, because our drone has bad eyesight and can't actually see the whole arena all the time.

Infact, it turns out that the Logitech C920 camera, snuggly mounted on the belly of our drone, has a vertical FOV of about 40 degrees. What this means is that, at a height of 3 metres (the maximum we are allowed to fly), we can only see about 2 meters worth of the ground along the screen vertical. We have a bit more reach horizontally, but we're considering worst cases here.

And that's at maximum height! We regularly need to stay low for quick access to the ground robots, which would only further diminish our sight. We are planning to mount cameras on the side that can see more of the arena, but we have yet to test how reliable the object recognition from those might be.

The goal of modelling the ground robots was motivated by the fact that if we could keep track of where robots are likely to be, by some internal book-keeping, we could make an educated guess about the best places to look for them. In this post I'll let you in on one of the approaches that we tried; how it works, and why it didn't work for us.

A welcome idea

After playing around with our super-cool simulator of the mission for some time, I got an intuition of how the robots move. Specifically, I noticed that they generally tend to stay on a straight line, moving back and forth. Every so often they hit something and stray from the path, but that doesn't happen all the time.

The following idea approached me in much the same way ideas tend to do - in the shower - and told me: "Hey, you should really use Gaussians". For those of you who are rusty with their statistics, a Gaussian you find in the wild usually looks something like this:

Gaussians often come knocking on your door when you deal with random systems, and are associated with what statisticians call "the normal distribution". Remarkably, alot of randomness that we can observe in nature tend to follow this distribution. For that reason it is usually a good guess for a distribution, if you have no idea which one is best for your problem.

The basis of my first approach was to divide the world into cells. Perhaps somewhat hastely, I thought that the pre-existing 1x1m grid cells marked up with tape would do. In each cell I would have a number between 0 and 1, indicating how much I believe there to be a ground robot in that cell.

Whenever the camera sees a ground robot, I would take note of where we saw it and which direction it was heading in. Using that information, and the fact that the ground robots do a planned reverse every 20 seconds, I could construct a straight-line path between the robot's two reversal points. When we then lost sight of the robot, I could do a simple line interpolation to estimate its position along the path.

Every 5 seconds, the robots will turn a small, random angle. Over time, these turns accumulate and make up a "random walk", causing the robot to stray from its path. To accomodate that fact, I wanted my estimates to become "less tight" over time. And that is where our revered mathematician Herr Gauss comes in. Instead of estimating a single point along the path, I would place a Gauss surface on it, with a center that moves back and forth. That would allow me to incorporate uncertainty into the estimate by widening the Gaussian over time.

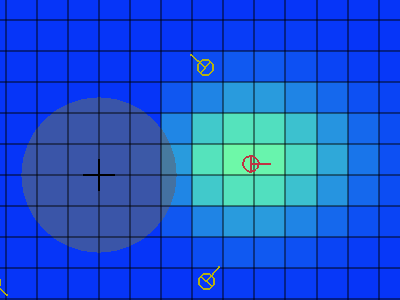
Brighter color indicates higher belief, while a dim color indicates low belief.

The animation above shows how this looks for tracking a single robot. We start out with a wide estimate, since we haven't seen the robot in a while. After a while it enters our field of vision, causing the estimate to tighten near the robot's center. Since all the sensors we use to estimate our position and do object-detection have uncertainty, the estimate leaks ever so slightly to neighboring cells.

Once we lose sight of the robot, the uncertainty grows again. It will continue growing until it becomes a soup of entropy, much like the cosmic background radiation which surrounds us. Always. Everywhere.

Belief or superstition?

The above animation may lead you to believe that this actually works pretty well. Unfortunately, when you add 9 more robots into the mix, things turn ugly, fast. In the animation below, a particular interaction between the three robots occurs.

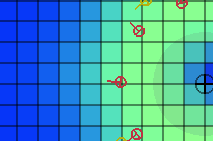
One of them collides with a tower robot, causing our path estimate to be completely off. When it comes back prematurely, we think we are seeing the robot on the left again, because it happened to have more overlap in its belief with what we are seeing. This triggers a phenomenom I've named Belief-Thieving, where one robot "steals" from another robot's probability density field, leading us to lose track of the left-side robot.

As time passes and the robots do their thing, complex interactions like this will happen. Unless we really strive to check up on the robots regularly, the estimates are going to be far off because of that. This led me to the following conclusion:

Keeping track of individual robots is hard!

Like, really hard. Seriously. At this point I started challenging the idea of even trying to do so in the first place. In the end, we don't really care where one specific robot is. What do we care about then, you ask? How can we guide the search without keeping track of individuals? Well that is a very good question indeed. So good, in fact, that it will be the topic of Ascend's next tech post.

Don't want to miss it? Well, you can either wham on the F5 key every day until next week, or you can always subscribe to one of our social media channels with the slick little buttons at the end of this page.

Either way, until then, thanks for reading, and we'll see you in the future!